零散的笔记
Gumbel-Softmax
常规的 softmax 直接建模了一个概率分布(多项分布),基于交叉熵的训练准则使分布尽可能靠近目标分布;而 gumbel-softmax 则是对多项分布采样的一个近似。使用上,常规的有监督学习任务(分类器训练)中,直接学习输出的概率分布是自然的选择;而对于涉及采样的学习任务(VAE 隐变量采样、强化学习中对actions 集合进行采样以确定下一步的操作),gumbel-softmax 提供了一种再参数化的方法,使得模型可以以端到端的方式进行训练。
个人Takeaway:为了采样,logits加上GumbelNoise,使得采样带有随机性的同时采样概率严格符合logits(或者说log prob)的prob的分布,现在得到的版本是Gumbel-Max;同时为了使得可导,使用GumbelSoftmax替代原本的argmax。
ELO Rating
ELO算法基于这样一种假设:一名选手的当前实力受各种因素的影响会在一定范围内波动,某个时刻的用来描述其实力的函数应当符合正态分布:
这里的U是选手的真实实力,是选手实力的波动范围(实力的稳定性)。
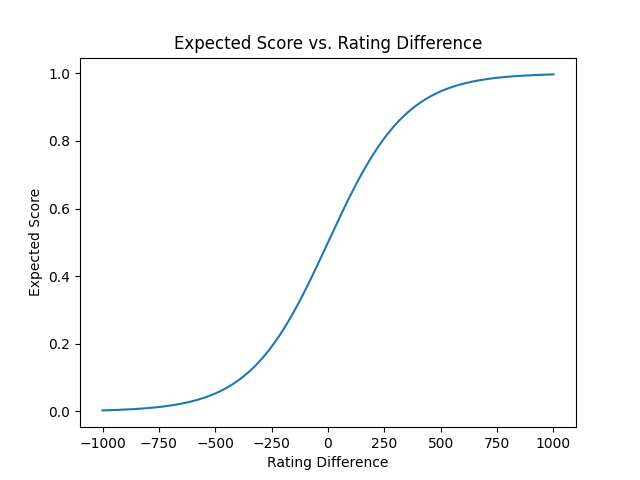
经过计算,可以得出两名选手进行对战时的预期胜率:
D为两名选手实力的差值。实际工程中我们使用以下函数进行近似代替:
胜率与分差的关系图如下:
ok,比方说我们现在开始了一个新的赛季,每个人的初始分数都是1200,那么在赛季结束时,或者说每一局游戏之后每个玩家的分数如何更新呢?
我们有如下公式:
其中是新的分数,是旧的分数,K是一个常数,W是实际的比赛结果(1代表胜利,0代表失败),P(D)是预期的胜率。
举一个实际例子,赛季刚开始A和B的分数都是1200,,K=32,A赢了,那么A的分数变为: B的分数变为: 以此类推。
ELO积分对玩家水平的精确指示会打击玩家的信心,分值收敛结束后,再进行更多的对局几乎不会有任何提高(除非找了代练或者自己不知道为啥突然打通任督二脉)。
所以我们将玩家真实水平隐藏,并用一些模糊柔和的方式去告诉玩家他当前的水平(按照ELO分数包装为青铜白银黄金白金钻石)。
但记得,ELO分不会消失,从显示变成了隐藏,我们的一切计算还是以ELO分数为依据。
UCB
推荐阅读:
Upper Confidence Bound Algorithm in Reinforcement Learning UCB1的代码实现
class UCB1():
def __init__(self, counts, values):
self.counts = counts # Count represent counts of pulls for each arm. For multiple arms, this will be a list of counts.
self.values = values # Value represent average reward for specific arm. For multiple arms, this will be a list of values.
return
# Initialise k number of arms
def initialize(self, n_arms):
self.counts = [0 for col in range(n_arms)]
self.values = [0.0 for col in range(n_arms)]
return
# UCB arm selection based on max of UCB reward of each arm
def select_arm(self):
n_arms = len(self.counts)
for arm in range(n_arms):
if self.counts[arm] == 0:
return arm
ucb_values = [0.0 for arm in range(n_arms)]
total_counts = sum(self.counts)
for arm in range(n_arms):
bonus = math.sqrt((2 * math.log(total_counts)) / float(self.counts[arm]))
ucb_values[arm] = self.values[arm] + bonus
return ucb_values.index(max(ucb_values))
# Choose to update chosen arm and reward
def update(self, chosen_arm, reward):
self.counts[chosen_arm] = self.counts[chosen_arm] + 1
n = self.counts[chosen_arm]
# Update average/mean value/reward for chosen arm
value = self.values[chosen_arm]
new_value = ((n - 1) / float(n)) * value + (1 / float(n)) * reward
self.values[chosen_arm] = new_value
return
MTCS
蒙特卡洛树搜索(Monte Carlo tree search)简称MCTS,和一般的蒙特卡洛方法不是一个概念。通俗的理解,蒙特卡洛方法是随机现象中用频率来近似概率,模拟次数越多,结果越准确。而蒙特卡洛树搜索,是减少某些决策过程的模拟次数的一种算法,是一种启发式算法。最引人注目的应用是计算机围棋程序,也可用于其他棋盘游戏、电子游戏以及不确定性游戏。
所谓启发式算法,是相对于最优化算法而言。最优化算法,一般是通过计算得到问题的最优解;而启发式算法,往往也是解决优化问题,但是一种基于直观或经验构造出的算法,一般给出的是问题的可行解,与最优解可能会有偏离。
下面以计算机围棋程序为例,通过介绍如何让计算机学好下围棋,说明蒙特卡洛树搜索。
在计算机与对手对弈围棋中,给定了一个围棋状态,如果想让计算机知道,这步棋怎么走对自己最有利,最后取得胜利的机会最大,理论上可以建立一颗树:
将给定的棋盘状态作为根节点,这是第一层;
将这个状态下可以选择的动作(棋的走法)列出,将动作后的状态作为节点,放在根节点的下一层,作为第二层,根节点与子节点的连线,分别表示走子的动作。(后面的叙述,均以节点表示棋盘的状态,相应的连线表示动作。)
当然,计算机无论选择第二层哪一个动作,走完之后,对方都会相应的也走一步棋,改变了棋盘的状态,计算机根据每个新的状态,又会有新的相应走法,把这些新动作的状态列出来,作为子节点放在第二层对应节点的下边,这就是第三层。
依此类推,一直往下,直至棋局结束分出胜负,就形成了一个树,简称决策树
判断当前这步棋怎么走才好,理论上可以从上向下逐层逐节点的进行仿真计算,即每个节点都从本身的状态开始,与对手模拟对弈,直至分出胜负。反复进行多次,即可统计出这步棋的好坏,通过各个节点的比较,则可找到最好的走法。这也是用频率来近似概率,是一种蒙特卡洛方法。
但是,这样逐个节点的反复模拟对弈,计算量会大的惊人,当前的计算机根本承受不了。
因此,需要找到一种既有效又可行的办法。
蒙特卡洛树搜索决定每步棋怎么走,也是要和对方模拟对弈,但不是所有的走法都模拟,而是选择胜算较高的节点进行模拟对弈,而且不仅模拟当前状态,还要向后多走几步进行模拟,最后找到这步棋的最优走法,其特点可以说就是这个选择性。
就是说,蒙特卡洛树搜索方法也是建立一个决策树,但其节点一般是由胜算较高的节点构成。想一下人类棋手走棋,每走一步棋也不是所有的走法都考虑,也是凭经验选择胜算较高的走法进行比较,也是要往后多计算几步。
蒙特卡洛树搜索的的工作步骤,一般有四步:
(1)选择(Selection):从根节点开始,根据一定的策略(比如UCB公式),向下选择子节点,直到找到叶子节点。
(2)扩展(Expansion):对叶子节点进行扩展,生成新的子节点。在围棋程序中,扩展的子节点一般是由神经网络生成的。
(3)模拟(Simulation):对新生成的子节点进行模拟对弈。模拟可以采用随机模拟,或者使用神经网络模型进行快速评估,目的是得到新节点的胜负结果。
(4)反向传播(Backpropagation):将模拟得到的结果通过回溯的方式,更新所有经过的节点的统计信息,包括模拟对弈次数、获胜次数等。
反复的重复上述步骤,蒙特卡洛的搜索树不断的扩展,树中的数据不断的更新,各步棋的优劣信息不断汇总到根节点,最终得到潜力最高的节点,作为最终的决策。

下面是对于四个步骤的详细解释:
- 选择(Selection)
在选择阶段,需要从根节点,也就是要做决策的局面R出发向下选择出一个最急迫需要被拓展的节点N,局面R是是每一次迭代中第一个被检查的节点;对于被检查的局面而言,他可能有三种可能:
(1)该节点所有可行动作都已经被拓展过
(2)该节点有可行动作还未被拓展过
(3)这个节点游戏已经结束了(例如已经连成五子的五子棋局面)
对于这三种可能:
(1)如果所有可行动作都已经被拓展过了,那么我们将使用UCB公式计算该节点所有子节点的UCB值,并找到值最大的一个子节点继续检查。反复向下迭代。
(2)如果被检查的局面依然存在没有被拓展的子节点(例如说某节点有20个可行动作,但是在搜索树中才创建了19个子节点),那么我们认为这个节点就是本次迭代的的目标节点N,并找出N还未被拓展的动作A。执行步骤[2]
(3)如果被检查到的节点是一个游戏已经结束的节点。那么从该节点直接执行步骤[4]。每一个被检查的节点的被访问次数在这个阶段都会自增。在反复的迭代之后,我们将在搜索树的底端找到一个节点,来继续后面的步骤。
- 拓展(Expansion)
在选择阶段结束时候,我们查找到了一个最迫切被拓展的节点N,以及他一个尚未拓展的动作A。在搜索树中创建一个新的节点Nn作为N的一个新子节点。Nn的局面就是节点N在执行了动作A之后的局面。
- 模拟(Simulation)
为了让Nn得到一个初始的评分。我们从Nn开始,让游戏随机进行,直到得到一个游戏结局,这个结局将作为Nn的初始评分。一般使用胜利/失败来作为评分,只有1或者0。反向传播(Back Propagation)在Nn的模拟结束之后,它的父节点N以及从根节点到N的路径上的所有节点都会根据本次模拟的结果来添加自己的累计评分。如果在[1]的选择中直接发现了一个游戏结局的话,根据该结局来更新评分。每一次迭代都会拓展搜索树,随着迭代次数的增加,搜索树的规模也不断增加。当到了一定的迭代次数或者时间之后结束,选择根节点下最好的子节点作为本次决策的结果。
#!/usr/bin/env python
import random
import math
import hashlib
import logging
import argparse
"""
A quick Monte Carlo Tree Search implementation. For more details on MCTS see See http://pubs.doc.ic.ac.uk/survey-mcts-methods/survey-mcts-methods.pdf
The State is a game where you have NUM_TURNS and at turn i you can make
a choice from an integeter [-2,2,3,-3]*(NUM_TURNS+1-i). So for example in a game of 4 turns, on turn for turn 1 you can can choose from [-8,8,12,-12], and on turn 2 you can choose from [-6,6,9,-9]. At each turn the choosen number is accumulated into a aggregation value. The goal of the game is for the accumulated value to be as close to 0 as possible.
The game is not very interesting but it allows one to study MCTS which is. Some features
of the example by design are that moves do not commute and early mistakes are more costly.
In particular there are two models of best child that one can use
"""
#MCTS scalar. Larger scalar will increase exploitation, smaller will increase exploration.
SCALAR=1/(2*math.sqrt(2.0))
logging.basicConfig(level=logging.WARNING)
logger = logging.getLogger('MyLogger')
class State():
NUM_TURNS = 10
GOAL = 0
MOVES=[2,-2,3,-3]
MAX_VALUE= (5.0*(NUM_TURNS-1)*NUM_TURNS)/2
num_moves=len(MOVES)
def __init__(self, value=0, moves=[], turn=NUM_TURNS):
self.value=value
self.turn=turn
self.moves=moves
def next_state(self):
nextmove=random.choice([x*self.turn for x in self.MOVES])
next=State(self.value+nextmove, self.moves+[nextmove],self.turn-1)
return next
def terminal(self):
if self.turn == 0:
return True
return False
def reward(self):
r = 1.0-(abs(self.value-self.GOAL)/self.MAX_VALUE)
return r
def __hash__(self):
return int(hashlib.md5(str(self.moves).encode('utf-8')).hexdigest(),16)
def __eq__(self,other):
if hash(self)==hash(other):
return True
return False
def __repr__(self):
s="Value: %d; Moves: %s"%(self.value,self.moves)
return s
class Node():
def __init__(self, state, parent=None):
self.visits=1
self.reward=0.0
self.state=state
self.children=[]
self.parent=parent
def add_child(self,child_state):
child=Node(child_state,self)
self.children.append(child)
def update(self,reward):
self.reward+=reward
self.visits+=1
def fully_expanded(self, num_moves_lambda):
num_moves = self.state.num_moves
if num_moves_lambda != None:
num_moves = num_moves_lambda(self)
if len(self.children)==num_moves:
return True
return False
def __repr__(self):
s="Node; children: %d; visits: %d; reward: %f"%(len(self.children),self.visits,self.reward)
return s
def UCTSEARCH(budget,root,num_moves_lambda = None):
for iter in range(int(budget)):
if iter%10000==9999:
logger.info("simulation: %d"%iter)
logger.info(root)
front=TREEPOLICY(root, num_moves_lambda)
reward=DEFAULTPOLICY(front.state)
BACKUP(front,reward)
return BESTCHILD(root,0)
def TREEPOLICY(node, num_moves_lambda):
#a hack to force 'exploitation' in a game where there are many options, and you may never/not want to fully expand first
while node.state.terminal()==False:
if len(node.children)==0:
return EXPAND(node)
elif random.uniform(0,1)<.5:
node=BESTCHILD(node,SCALAR)
else:
if node.fully_expanded(num_moves_lambda)==False:
return EXPAND(node)
else:
node=BESTCHILD(node,SCALAR)
return node
def EXPAND(node):
tried_children=[c.state for c in node.children]
new_state=node.state.next_state()
while new_state in tried_children and new_state.terminal()==False:
new_state=node.state.next_state()
node.add_child(new_state)
return node.children[-1]
#current this uses the most vanilla MCTS formula it is worth experimenting with THRESHOLD ASCENT (TAGS)
def BESTCHILD(node,scalar):
bestscore=0.0
bestchildren=[]
for c in node.children:
exploit=c.reward/c.visits
explore=math.sqrt(2.0*math.log(node.visits)/float(c.visits))
score=exploit+scalar*explore
if score==bestscore:
bestchildren.append(c)
if score>bestscore:
bestchildren=[c]
bestscore=score
if len(bestchildren)==0:
logger.warn("OOPS: no best child found, probably fatal")
return random.choice(bestchildren)
def DEFAULTPOLICY(state):
while state.terminal()==False:
state=state.next_state()
return state.reward()
def BACKUP(node,reward):
while node!=None:
node.visits+=1
node.reward+=reward
node=node.parent
return
if __name__=="__main__":
parser = argparse.ArgumentParser(description='MCTS research code')
parser.add_argument('--num_sims', action="store", required=True, type=int)
parser.add_argument('--levels', action="store", required=True, type=int, choices=range(State.NUM_TURNS+1))
args=parser.parse_args()
current_node=Node(State())
for l in range(args.levels):
current_node=UCTSEARCH(args.num_sims/(l+1),current_node)
print("level %d"%l)
print("Num Children: %d"%len(current_node.children))
for i,c in enumerate(current_node.children):
print(i,c)
print("Best Child: %s"%current_node.state)
print("--------------------------------")