Generative Modeling by Estimating Gradients of the Data Distribution

这篇论文发表早于DDPM,但是任务跟DDPM一样——生成图像。涉及到的关键词为:
- 朗之万采样
- Score Matching
你可能对这两个名词一头雾水,别着急,在具体看论文算法之前,我们先铺垫一下。
1. 朗之万采样
首先,它是一种采样方法。什么意思呢?就是给定一个已知的概率分布,通过采样的方式,得到这个概率分布的样本。
那你可能会问,干嘛不直接随机均匀采样就好了?这里需要考虑到实际数据分布的一些特点:随机采的数据点大概率是。所以现在的问题就是,我们采样得到的数据点需要尽可能“合理”。
ok,朗之万采样提供了一个解决方案,我们从一个数据点开始,经过如下方程的若干次迭代之后,便可以得到一个合理的采样点:

刨除噪声项,其实朗之万采样就是一个朝着pdf最大的方向进行采样的过程——这样也就能保证采样得到的数据点尽可能“合理”。
看到这里,我们给出一个实际例子方便理解。我们从[-3, 3]中均匀采样10000个点,每一个点都按照前面的朗之万迭代的方式更新100次得到最终的点。 可以看到,一开始均匀采样的点并不能很好的体现pdf的形状,但是经过朗之万采样之后,pdf的形状就出现了。
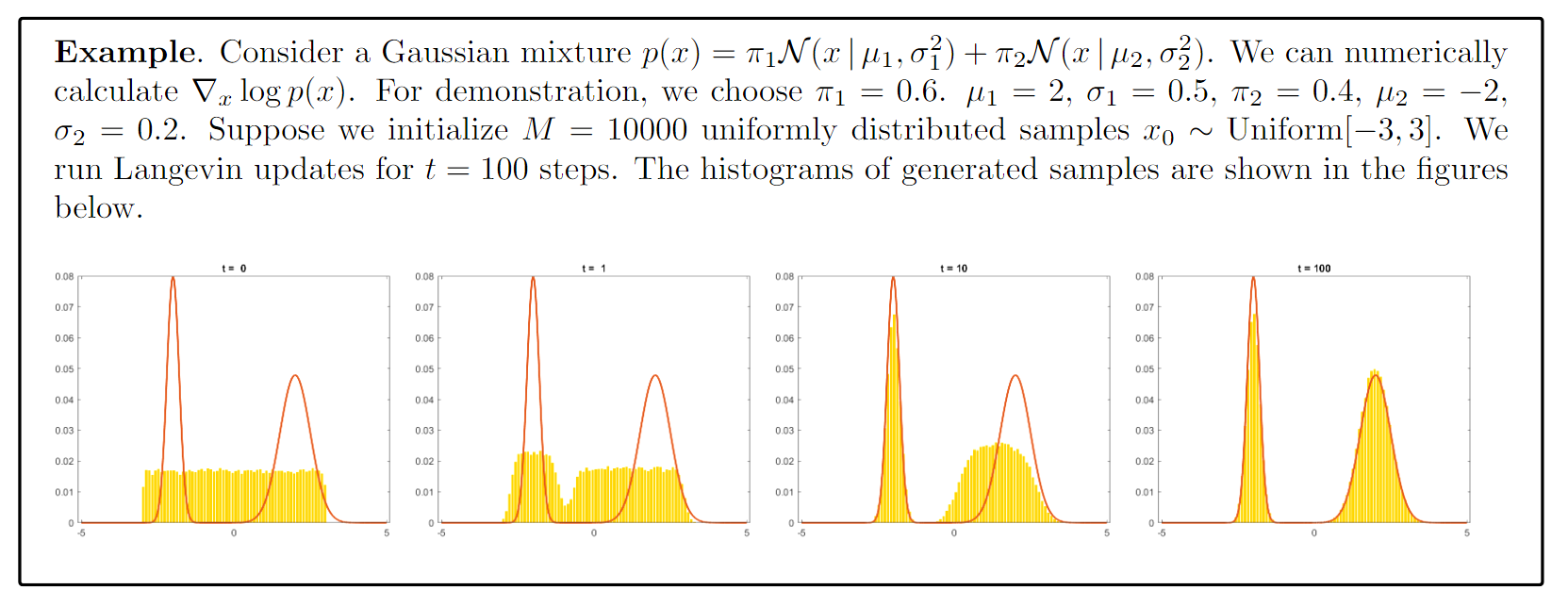
总结:朗之万采样是一个迭代式地更新一开始不那么“好”的采样点,使之更“合理”的过程。这个过程可以理解成梯度上升的思路。
诶看到这里,你可能会很好奇,前面那个迭代式是怎么算出来的?我这里放出一个博客的证明,我自己就不证明了:
总结:朗之万采样方法告诉我们,如果我们通过某些方式知道了(近似了),那么即使我们不知道,我们依旧可以进行“合理”采样。而接下来我们将会介绍如何使用Score Matching来近似得到。论文片段:

看点代码:
def Langevin_dynamics(self, x_mod, scorenet, n_steps=200, step_lr=0.00005):
images = []
labels = torch.ones(x_mod.shape[0], device=x_mod.device) * 9
labels = labels.long()
with torch.no_grad():
for _ in range(n_steps):
images.append(torch.clamp(x_mod, 0.0, 1.0).to('cpu'))
noise = torch.randn_like(x_mod) * np.sqrt(step_lr * 2)
grad = scorenet(x_mod, labels)
x_mod = x_mod + step_lr * grad + noise
x_mod = x_mod
print("modulus of grad components: mean {}, max {}".format(grad.abs().mean(), grad.abs().max()))
return images
2. Score Matching
第一小节中,我们介绍了朗之万采样,定义,便是所谓的score function。假设我们通过某种方式训练得到来近似,那么我们便可以使用朗之万采样方式进行采样了。
下图为一个高斯混合分布以及其score function。看看y=0与score function的交点,你发现什么没有?
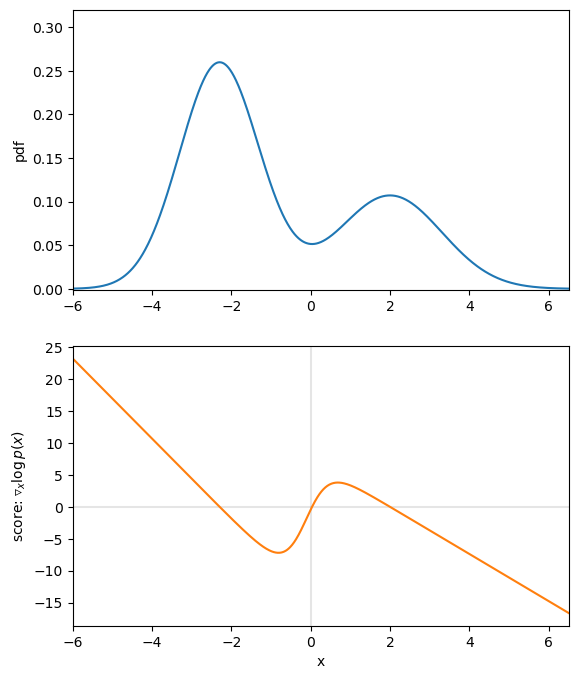
分析至此,你发现问题没有,我们明明要求的是数据集的分布,但是你现在把当成是已知,这不是很奇怪吗?
别急,我们慢慢来。假设给定数据集,使用核密度估计,定义:
我们使用已知的数据集和近似,则我们训练神经网络来拟合。其损失为:
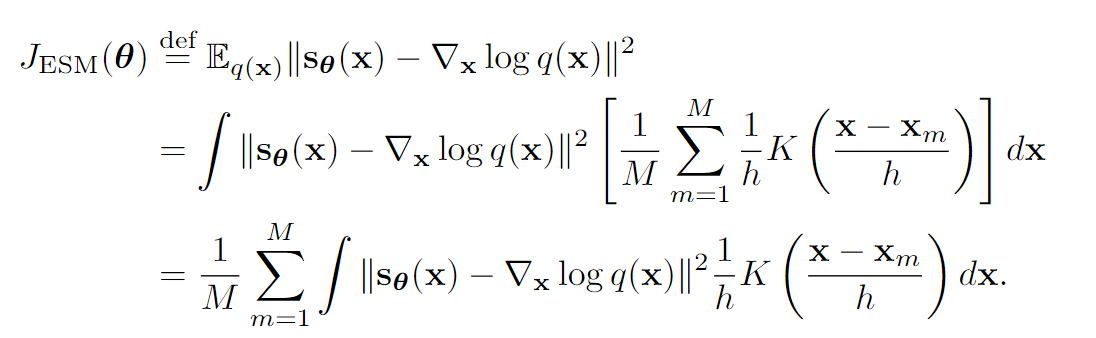
用KDE估计的缺点是效果比较差。Estimation of Non-Normalized Statistical Models by Score Matching这篇论文通过一定的等价变形将MSE中的真实score一项消掉了,其的出来的损失函数为(推导见知乎推文,在Score Matching这篇论文中也提到了这个,叫做Sliced Score Matching:
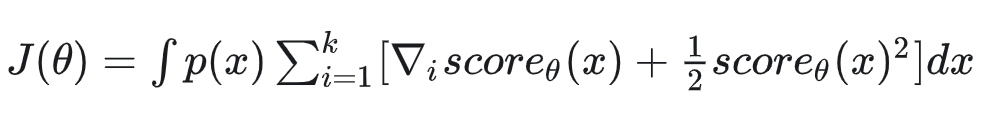
下面介绍另一个方法:Denoising Score Matching,也是论文中使用的方法。我们先讲这个方法,随后在第三小节我们再解释原因。
给数据加噪音,获得,这一步可以理解成数据增强,即,其中。
于是我们的损失可以化简为:
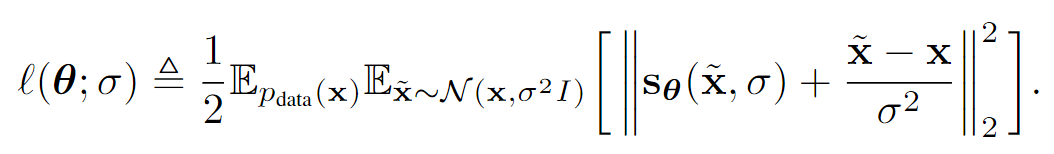
看点代码:
def dsm_score_estimation(scorenet, samples, sigma=0.01):
perturbed_samples = samples + torch.randn_like(samples) * sigma
target = - 1 / (sigma ** 2) * (perturbed_samples - samples)
scores = scorenet(perturbed_samples)
target = target.view(target.shape[0], -1)
scores = scores.view(scores.shape[0], -1)
loss = 1 / 2. * ((scores - target) ** 2).sum(dim=-1).mean(dim=0)
return loss
3. 解释第二小节,为什么要引入噪声,损失函数为什么那么写?(对样本进行perturb)
第一个原因:
我们的样本空间实际上只是高维空间中的一个流形子空间,高维空间中的绝大多数点都是,如果只是在样本空间上学习score function,这意味着我们只会在样本空间上学好score function,对于稍微偏离的点,score function将会是不准的,而score function不准将会导致我们朗之万采样的采样效果不好。这样子,即使是working space中的点,score function的“准”性也会变差。所以给每一个样本点加噪声主要是使得score function在空间中的“覆盖面”更大,从而能保证score function的“准”性。
第二个原因:
我们之前说真实s(x)并不知道,但是其实通过加噪之后能够恰好进行有效化简,从而消掉真实s(x)项。
4. 实现上,用了退火采样
不同噪声强度都需要进行优化:

采样时,先迈大步子,再细粒度地走:
