QGPO: Contrastive Energy Prediction for Exact Energy-Guided Diffusion Sampling in Offline Reinforcement Learning

关键词：

• Offline RL
• Guided Diffusion(Classifier-Guided Diffusion)
• Energy-Guided Diffusion

读这篇论文之前，请确保你详细阅读过Diffuser及其代码。

我们这里简单的描述一下Diffuser的Guided的过程：

• 使用BC的范式训练behavior policy：$\mu(a|s)$或者说$\epsilon_{\theta}(s, a, t)$
• 使用MSE的范式训练value model：$V_{\phi}(s, a, t)$，具体是用的是轨迹的return作为训练目标。

Diffuser Guided的方式是：

本文与Diffuser的范式有点类似，但是有以下几点不同之处：

• 没有在轨迹层面建模policy，更多的是类似于DQL或者说SfBC的behavior policy的方式
• Guided的方式不再是Diffuser的任何中间状态的V都是用轨迹return作为target进行MSE训练得到的所谓的Classifier，而是使用了contrastive energy model的方式学习（这块比较难懂，后面再详细解说）

Motivation

$\max_{\pi} \mathbb{E}_{\mathbf{s} \sim \mathcal{D}_{\mu}} \left[ \mathbb{E}_{\mathbf{a} \sim \pi(\cdot | \mathbf{s})} Q_{\psi}(\mathbf{s}, \mathbf{a}) - \frac{1}{\beta} D_{\mathrm{KL}} \left(\pi(\cdot | \mathbf{s}) \| \mu(\cdot | \mathbf{s})\right) \right]$

最优策略： $\pi^*(a|s) \propto \mu(a|s) e^{\beta Q(s,a)}$

假设我们现在用Diffusion Model按照BC的方式学习了$\mu(a|s)$，按照传统的TD-Learning的方式学习了$Q(s,a)$，那么最优策略呢？

这里最难的一点是因为$\mu(a|s) e^{\beta Q(s,a)}$这个分布是未归一化的，因此直接从$\pi^*(a|s)$中采样动作貌似比较麻烦。当然，一个简单的办法便是Monte Carlo采样，这就是SfBC的做法，但是由于Diffusion Model的采样效率的问题，SfBC的采样效率比较差。

另外，由于Diffusion Model采样中有中间时间步，因此为了更加有效的Guided，其实是需要学习一个所谓的中间态的Q函数，即$Q(s, a, t)$，注意这里的t是Diffusion Model的采样时间步，而不是原始的轨迹时间步。为了让大家对这个采样过程更加清楚，作者在论文也给出了一个示例：

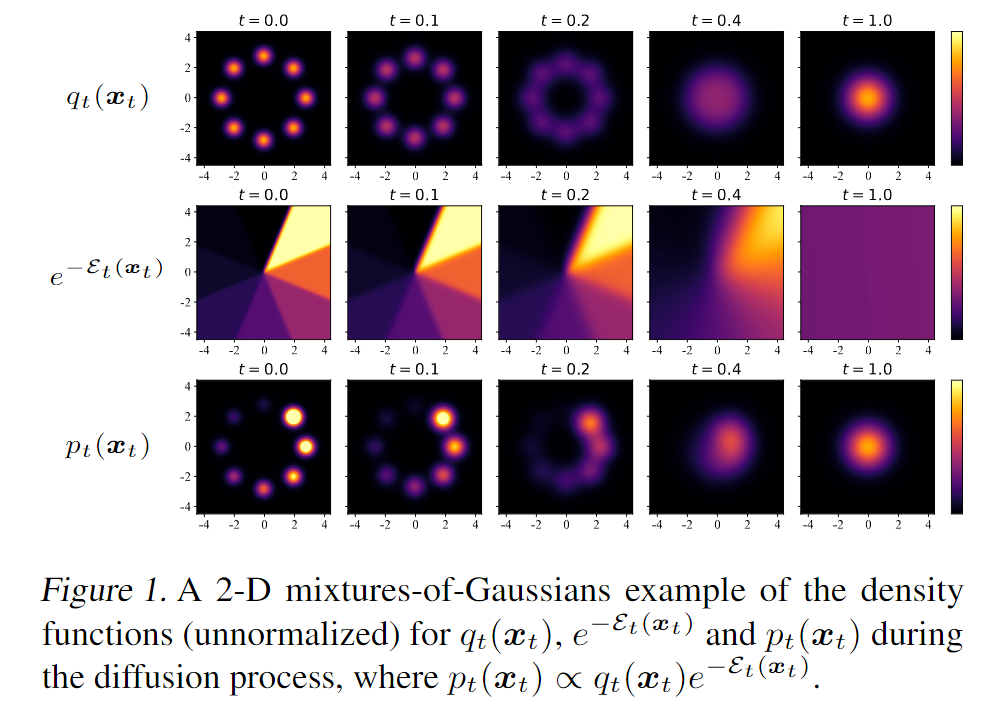
假设我们现在已经学到了$Q(s, a, t)$，那么我们的采样过程便可以按照如下方式（只写了梯度，但是对于Score Matching比较熟悉的同学，这个式子应该是足够了）：

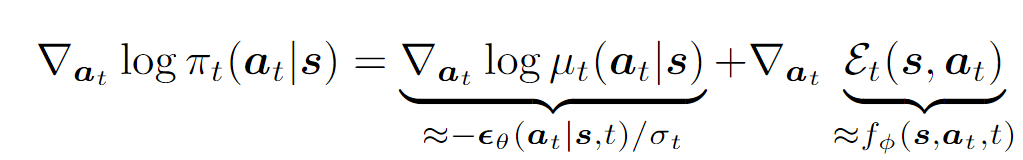
为什么要引入能量？能量模型 vs 概率模型？

概率模型是能量模型的一个特例。能量可以看作没有正则化的负对数概率。

为什么用能量模型而不是概率模型？

• 能量模型在打分函数的选择上更加灵活
• 学习的目标函数的选择更加灵活
• 能量和概率的转换： Gibbs-Boltzmann分布

中间态Q函数？中间态能量？

TBD：

ok，说白了，难点就是中间状态的能量密度怎么求出来？

跟对比损失的区别，对比损失更多强调的是正样本和负样本之间的一个对比，损失里面只需要把正样本相比于其它负样本区分开就行了。

但是QGPO相当于是正

一些本质上共通的Paper：

• 朱军老师团队的另一篇类似的Paper
• Offline Transition Modeling via Contrastive Energy Learning