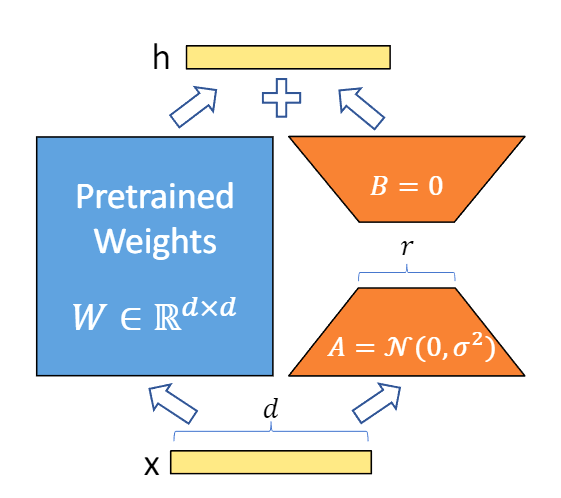
LoRA

和其它串行的适配器算法不同, LoRA的做法是在LLM的某些矩阵 $\left(W\in \mathbb{R}^{d\times k}\right)$ 旁插入一个和它并行的新的权值矩阵$\Delta W\in \mathbb{R}^{d\times k}$ ，但是因为模型的低秩性的存在,我们可以将 $\Delta W$ 拆分成降维矩阵 $A\in \mathbb{R}^{r\times k}$ 和升维矩阵 $B\in \mathbb{R}^{d\times r}$，其中 $r\ll\min(d, k)$ ，从而实现了以极小的参数数量训练LLM。在训练时，我们将LLM的参数固定，只训练矩阵 A和B。根据式(1)，在模型训练完成之后，我们可以直接将 A和 B加到原参数上，从而在推理时不会产生额外的推理时延。

$h=W_0 x+\Delta W x=\left(W_0+\Delta W\right) x=W x+B A x, (1)$