IQ-Learn: Inverse soft-Q Learning for Imitation

NeurIPS 2021 spotlight paper: IQ-Learn: Inverse soft-Q Learning for Imitation

值得反复琢磨的paper！

Max Entropy Inverse Reinforcement Learning

在介绍IQ-Learn之前，我们先来回顾一下Max Entropy Inverse Reinforcement Learning。这个在GAIL论文中进行详细推导，我们这里仅仅只是简单回顾一下。

对于一个凸正则函数：$\psi: \mathbb{R}^{\mathcal{S}\times\mathcal{A}}\rightarrow \mathbb{\bar{R}}$，该函数作为正则化项，用于评估一个rewrad函数的复杂程度。我们可以定义一个Max Entropy Inverse Reinforcement Learning的目标函数如下： $\min_{\pi}\max_{r} L(\pi, r) = \mathbb{E}_{\rho_E}[r(s, a)] - \mathbb{E}_{\rho_{\pi}}[r(s, a)] - H(\pi)-\psi(r)$

其中，$\rho_E$是专家策略的分布，$\rho_{\pi}$是学习到的策略的分布，$H(\pi)$是策略的熵，$\psi(r)$是reward函数的复杂度。

怎么理解这个目标呢？

首先先看内层的目标： $\max_{r} L(\pi, r) = \mathbb{E}_{\rho_E}[r(s, a)] - \mathbb{E}_{\rho_{\pi}}[r(s, a)] - \psi(r)$

其表示当$\rho_{\pi}$或者说$\pi$固定时，我们希望专家策略在这个reward函数下的期望值要尽可能大于学习到的策略在这个reward函数下的期望值，而同时这个函数r不能过于复杂，因此加了一个正则化项$\psi(r)$。

外层的目标就不难理解了，当$r$固定时，我们希望学习到的策略的熵和期望表现要尽可能大，即最大化$\mathbb{E}_{\rho_{\pi}}[r(s, a)] + H(\pi)$。

而GAIL则证明了，上面的目标可以写成以下形式： $\min_{\pi} d_{\psi}(\rho_E, \rho_{\pi}) - H(\pi)$ 其中，$d_{\psi}(\rho_E, \rho_{\pi}) = \psi^*(\rho_E - \rho_{\pi})$，这里的$\psi^*$是$\psi$的Fenchel共轭函数。

共轭函数的定义为： $\psi^*(y) = \max_{x} \{y^Tx - \psi(x)\}$

Inverse soft Bellman Operator

我们都知道，Soft Bellman Operator是SAC中的核心，其定义如下： $Q_{\pi}(s, a) = r(s, a) + \gamma \mathbb{E}_{s'\sim p(s'|s, a)}[V_{\pi}(s')]$

其中，$V_{\pi}(s) = \mathbb{E}_{a\sim \pi(a|s)}[Q_{\pi}(s, a) - \alpha \log \pi(a|s)]$。

Imitation Learning的目标是学习一个reward函数，使得学习到的策略的行为尽可能接近专家策略的行为。因此，我们可以定义一个Inverse soft Bellman Operator： $r(s, a) = Q_{\pi}(s, a) - \gamma \mathbb{E}_{s'\sim p(s'|s, a)}[V_{\pi}(s')]$

也就是说，我们如果知道了$Q_{\pi}$和$V_{\pi}$，我们就可以通过上面的公式学习到reward函数。我们把这样的算子称为Inverse soft Bellman Operator，记作$\mathcal{T}^{\pi}: \mathbb{R}^{\mathcal{S}\times\mathcal{A}}\rightarrow \mathbb{R}^{\mathcal{S}\times\mathcal{A}}$。

后文的写法中,$(\mathcal{T}^{\pi}Q)(s, a)$表示$\mathcal{T}^{\pi}$作用在$Q$上的结果。

直觉告诉我们，$\mathcal{T}^{\pi}$是一个双射算子，即对于任意的$Q$，$\mathcal{T}^{\pi}Q$都是唯一的。因此，我们可以通过迭代的方式来学习到$\mathcal{T}^{\pi}$的不动点，即reward函数。严格的证明我们这里就不展开了。

有了这样的观察，我们是不是可以考虑将原来的Max Entropy Inverse Reinforcement Learning的目标函数改写成以下形式：

$\mathcal{J}(Q, \pi) = \mathbb{E}_{\rho_E}[(\mathcal{T}^{\pi}Q)(s, a)] - \mathbb{E}_{\rho_{\pi}}[(\mathcal{T}^{\pi}Q)(s, a)] - H(\pi) - \psi(\mathcal{T}^{\pi}Q)$

ok，这个便是IQ-Learn的核心思想。我们希望学习到的$Q$和$\pi$使得$\mathcal{T}^{\pi}Q$尽可能接近专家策略的行为，同时$\mathcal{T}^{\pi}Q$不能过于复杂。

我们有如下事实： $\max_{Q}\min_{\pi} \mathcal{J}(Q, \pi) = \max_{r}\min_{\pi} L(\pi, r)$

根绝Soft Q-learning和SAC的推导，假设我们已经知道了Q，那么其实不管是使用soft Q-learning还是SAC，我们都可以很容易地得到$\pi$的闭式解！

$\pi_{Q}(a|s) = \frac{\exp(Q(s, a)}{\int \exp(Q(s, a))da}$

因此，$\max_{Q}\min_{\pi} \mathcal{J}(Q, \pi) = max_{Q} \mathcal{J}(Q, \pi_{Q})$，这个优化问题就变成了一个单变量的优化问题。

Drawing on connections between RL and energy-based models, we propose learning a single model for the Q-value. The Q-value then implicitly defines both a reward and policy function. This turns a difficult min-max problem over policy and reward functions into a simpler minimization problem over a single function, the Q-value.

我们并不急着继续将IQ-learn的算法流程，读者可以暂时抛开IQ-learn的细节，我们来看看$d_{\psi}(\rho, \rho_E)$与f-divergence的联系。

$d_{\psi}(\rho, \rho_E)$与f-divergence的联系

后面的分析是一个从一般到特殊，从抽象到具体的过程，因为我们即将“实例化”正则化函数$\psi$。

首先，$\psi(\mathcal{T}^{\pi}Q)$特殊化为：

$\psi_g(r) = \mathbb{E}_{\rho_E}[g(r(s, a))]$

其中g是一个$\mathbb{R}\rightarrow \mathbb{R}$的凸函数。你可以将$r$看成一个向量，那么g将这个向量的每一个值映射到一个新的值，得到一个新的向量$g(r)$，这个向量与专家策略的分布做内积，得到一个标量$\rho_E^Tg(r)$。这个式子表示我们衡量所学习的reward的复杂程度，是在专家的“状态-行为”占用度量下的期望。至于为什么不用策略$\pi$的占用度量呢？因为$\pi$本身也未知且在迭代中变化，并不稳定，而专家策略的占用度量是固定的。

这里便是我们的第一个具体化的地方。函数$g$将reward函数映射到一个向量，而$\rho_E$本身也可以看成一个向量，两个向量的内积便是我们的正则化项，所以也可以写成$\rho_E^Tg(r)$。在这个过程中，占用度量作为一个权重分配到reward函数上，最终用于评判我们的rewrad的复杂程度。

再具体一点，我们可以将$g$定义为：

$g(x) = \begin{cases} x - \phi(x) ,\text{if} x\in Dom(\phi)\\ \infty, otherwise \end{cases}$

这里$\phi$为凹函数，且$Dom$为$\phi$的有效定义域。读者可能对为什么突然抛出这样一个定义感到好奇，我们之后再做解释，现在读者只需要知道这样定义的$g$是一个凸函数即可。

理解g看起来很奇怪的定义需要引入f-divergence的概念：

$D_f(\rho||\rho_E) = \mathbb{E}_{\rho}f\left(\frac{\rho}{\rho_E}\right)$

引入共轭函数$f^*$，我们可以得到： $D_f(\rho||\rho_E) = \max_{q: \mathcal{X}\rightarrow \mathbb{R}} \mathbb{E}_{\rho_E}[q(x)] - \mathbb{E}_{\rho}[f^*(q(x))]$

将$q=-r$带入上式，我们可以得到： $D_f(\rho||\rho_E) = \max_{r} \mathbb{E}_{\rho_E}[-f^*(-r)] - \mathbb{E}_{\rho}[r]$

记$f^*(-r) = \phi(r)$，我们可以得到： $D_f(\rho||\rho_E) = \max_{r} \mathbb{E}_{\rho_E}[\phi(r)] - \mathbb{E}_{\rho}[r] = \max_{r} \rho_E^T\phi(r) - \rho^Tr$

回顾以下我们的$d_{\psi}(\rho, \rho_E)$的定义： $\begin{aligned} d_{\psi}(\rho, \rho_E) &= \psi^*(\rho_E - \rho)\\ &= \max_{r} (\rho_E - \rho)^Tr - \rho_E^Tg(r)\\ \end{aligned}$

让$d_{\psi}(\rho, \rho_E) = D_f(\rho||\rho_E)$，我们可以得到： $\begin{aligned} \max_{r} (\rho_E - \rho)^Tr - \rho_E^Tg(r) &= \max_{r} \rho_E^T\phi(r) - \rho^Tr \end{aligned}$ 推出： $g(r) = r - \phi(r)$

在这个过程中，我们成功地将$d_{\psi}(\rho, \rho_E)$等价变形为f-divergence的形式，这样我们就可以用f-divergence来衡量$\rho$和$\rho_E$的差异，同时正则化了reward函数。（这句话一定要读懂，不然没办法理解为什么要这么定义g）。

这个将$d_{\psi}(\rho, \rho_E)$与f-divergence联系起来的过程是不可谓不精妙！

因此，$d_{\psi}(\rho, \rho_E)$的定义可以最终写成： $\begin{aligned} d_{\psi}(\rho, \rho_E) &= \psi^*(\rho_E - \rho)\\ &= \max_{r} (\rho_E - \rho)^Tr - \psi_g(r)\\ &= \max_{r} \rho_E^Tr - \rho^Tr - \rho_E^Tg(r)\\ &= \max_{r} \rho_E^Tr - \rho^Tr - \rho_E^T(r - \phi(r))\\ &= \max_{r} \rho_E^T\phi(r) - \rho^Tr\\ & = \max_{r} \mathbb{E}_{\rho_E}[\phi(r(s, a))] - \mathbb{E}_{\rho}r(s, a) \end{aligned}$ 现在，我们选取不同的f-divergence，我们就可以得到不同的函数$\phi$。如下表：

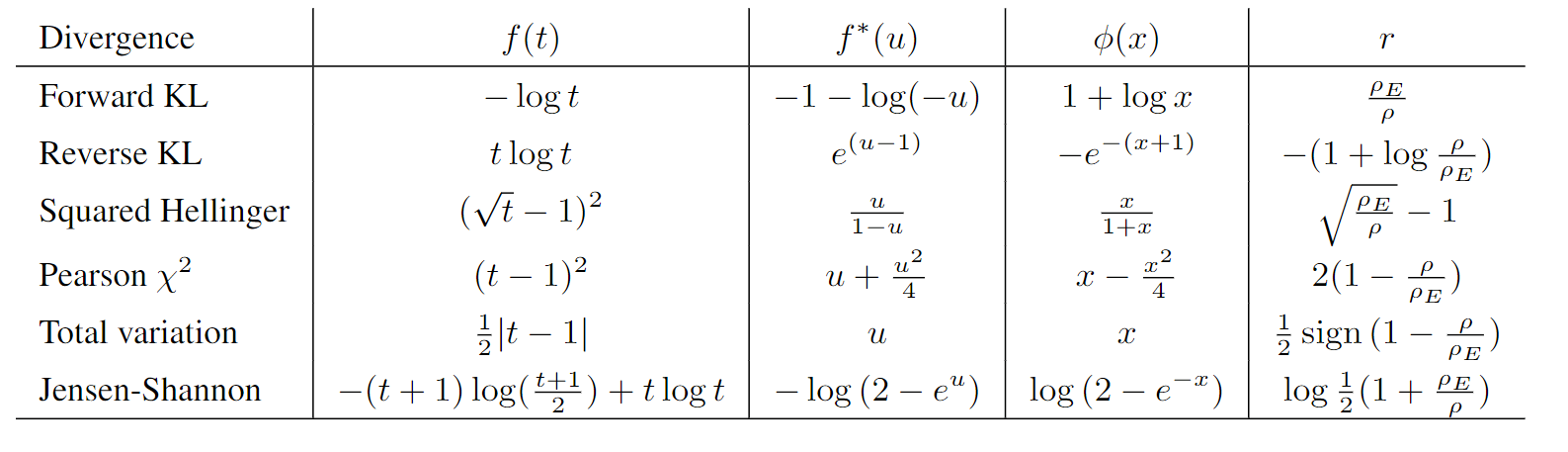
讲到这里，我们稍微回顾一下GAIL与本论文的理论上的关联，从本文视角下推导GAIL的目标函数：

将JS-divergence带入到$\max_{r} \rho_E^T\phi(r) - \rho^Tr$得到：$\max_{r} \rho_E^T\log(2-e^{-r}) - \rho^Tr$，看起来跟GAIL的$max_{D\in (0, 1)} \rho_E^T\log(D(s, a)) - \rho^T\log(1-D(s, a))$形式上是很相似了，通过待定系数便可以确定到$r$与D的关系式了，因此该r用在GAIL的policy作为其reward是合理的。

IQ-Learn算法流程

我们现在可以回到IQ-Learn的算法流程了。

最开始的最大化目标： $\mathcal{J}(Q, \pi) = \mathbb{E}_{\rho_E}[(\mathcal{T}^{\pi}Q)(s, a)] - \mathbb{E}_{\rho_{\pi}}[(\mathcal{T}^{\pi}Q)(s, a)] - H(\pi) - \psi(\mathcal{T}^{\pi}Q)$

经过若干处理之后得到的式子（化简并不是很难，请自行查阅论文证明部分）：

$\mathcal{J}(\pi, Q) = \mathbb{E}_{(s, a) \sim \rho_{E}}[Q(s,a) - \gamma \mathbb{E}_{s' \sim \mathcal{P}(\cdot | s,a)}V^\pi(s')] - (1- \gamma) \mathbb{E}_{s_0 \sim p_0}[V^\pi(s_0)] - \psi(\mathcal{T}^\pi Q)$

考虑到$\psi(\mathcal{T}^\pi Q) = \mathbb{E}_{\rho_{E}}[g(\mathcal{T}^\pi Q)]= \rho_{E}^Tg(\mathcal{T}^\pi Q)$，其中$g(x) = x - \phi(x)$，我们可以得到：

$\mathbb{E}_{\rho_{E}}[\phi(Q(s, a) - \gamma \mathbb{E}_{s' \sim \mathcal{P}(\cdot|s,a)}V^*(s'))] - (1- \gamma) \mathbb{E}_{\rho_0}[V^*(s_0)]$

至于怎么使用Q计算V，不同的范式会采用不同的方法，具体参见Soft-Q Learning和SAC的推导。

论文中使用了两种实验setting，分别是Online和Offline，对应的计算$(1- \gamma) \mathbb{E}_{s_0 \sim p_0}[V^\pi(s_0)]$这一项的方法也有所不同。

• Online：使用$\mathbb{E}_{(s, a, s')\sim replay(expert\ and \ policy)}[V(s) - \gamma V(s')]$
• Offline: 使用$\mathbb{E}_{(s, a, s')\sim expert}[V(s) - \gamma V(s')]$

不用$V^\pi(s_0)$的原因是在实验中观测到过拟合的现象。

使用$\chi^2$-divergence，我们可以得到$\phi(x) = -f^*(-x) = x-\frac{1}{4\alpha}x^2$,即$\psi(r)=\frac{1}{4\alpha}r^2$。

代码实现和简单实验验证

Offline IQ-Learn

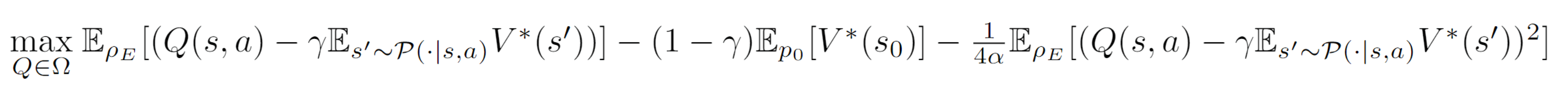
关键代码实现:

# χ2 divergence 
def offline_iq_loss(self, current_Q, current_v, next_v, batch):
    obs, action, reward, next_obs, done, truncated, is_expert = batch

    y = (1 - done) * self.gamma * next_v
    reward = (current_Q - y)[is_expert == 1]

    # -E_(ρE)[Q(s, a) - y]
    softq_loss = -reward.mean()

    # E_(ρE)[V(s) - γV(s')]
    value_loss = (current_v - y)[is_expert == 1].mean()

    # \psi(r)
    regularizer_loss = 1 / (4 * self.method_alpha) * (reward**2).mean()

    return softq_loss + value_loss + regularizer_loss

实验验证：

TBD

Online IQ-Learn

TBD

总结

IQ-Learn的思想就两点：

• 使用Q反过来表示reward函数
• $d_{\psi}(\rho, \rho_E)$与f-divergence的联系

这也是本文的行文思路。本文公式推导较多，请读者耐心阅读。