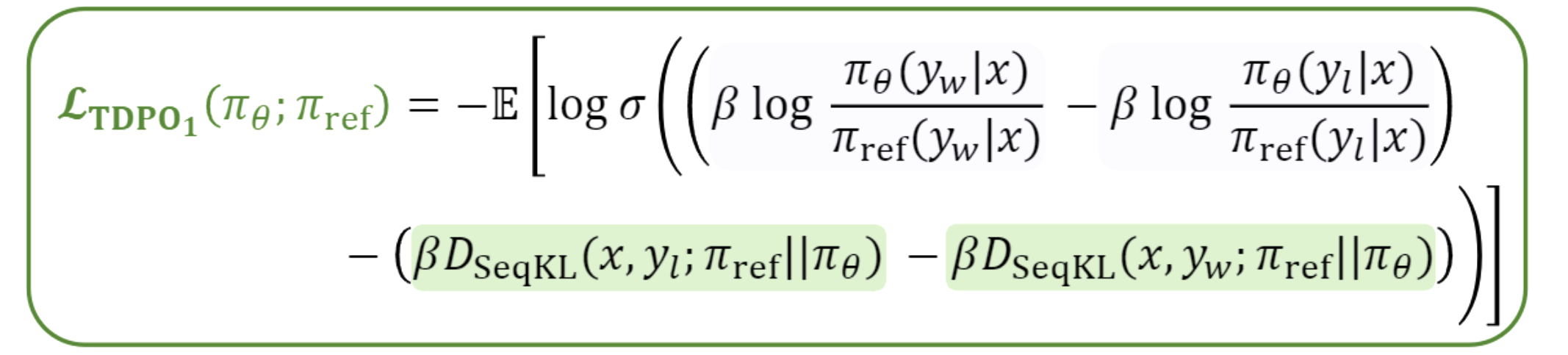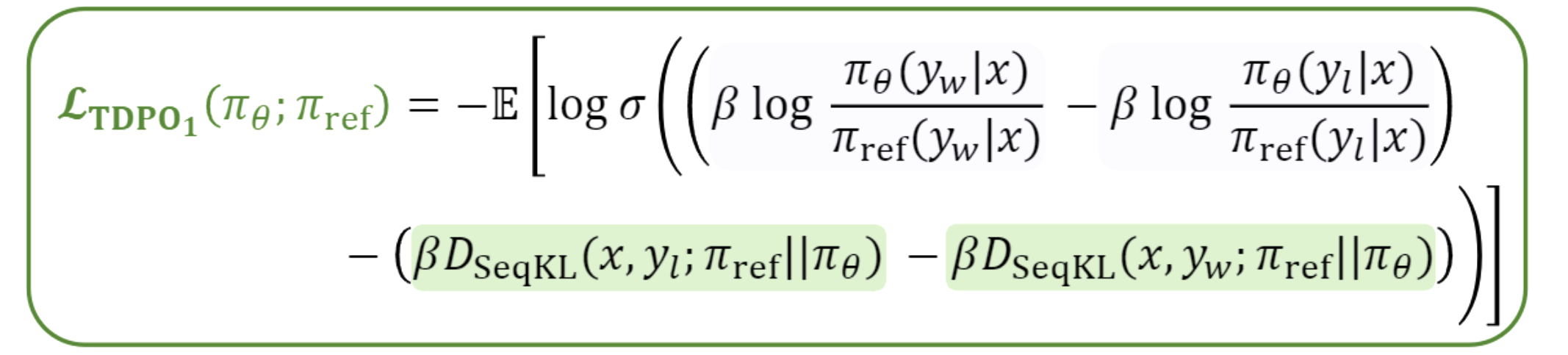TDPO

强化学习与LLM之间的符号关联说明

x代表prompt，y代表回答，二者均为序列。$y^t$代表y的第t个token，$y^{<t}$代表y的前t-1个token组成的序列。

定义状态$s_t=[x, y^{<t}]$，$a_t=y^t$，$r_t:=r(s_t, a_t) = r([x, y^{<t}], y^t)$

在LLM设定下，环境转移是完全确定的，给定当前的s和a，则s'为(s, a)的concat。

以下两种写法从一般到特殊：

RL:

$Q_{\pi}(s_t, a_t) = \mathbb{E}_{\pi}[\sum_{k=0}\gamma^kr_{t+k}|s_t, a_t]$

$V_{\pi}(s_t) = \mathbb{E}_{a_t\sim\pi(|s_t)}[Q_{\pi}(s_t, a_t)]$

$A_{\pi}(s_t, a_t)=Q_{\pi}(s_t,a_t)-V(s_t)$

LLM: $Q_{\pi}([x, y^{<t}], y^t) = \mathbb{E}_{\pi}[\sum_{k=0}\gamma^kr_{t+k}|[x, y^{<t}], y^t]$ $V_{\pi}([x, y^{<t}]) = \mathbb{E}_{y^t\sim\pi(|[x, y^{<t}])}[Q_{\pi}([x, y^{<t}], y^t)]$

$A_{\pi}([x, y^{<t}], y^t)=Q_{\pi}([x, y^{<t}],y^t)-V([x, y^{<t}])$

在本文设定下，$\gamma=1$。

逐步导出TDPO的目标

对于某一个状态$s=[x, y^{<t}]$，TDPO的优化目标为：

$\begin{aligned} max_{\pi_{\theta}} \mathbb{E}_{z\sim\pi_{\theta(|[x, y^{<t}], z)}}[A_{\pi_{ref}}([x, y^{<t}])],\\ \text{subject to: } D_{KL}(\pi_{\theta}||\pi_{ref}) \leq \epsilon \end{aligned}$

这个形式其实并不少见，TRPO和AWR论文中均出现了非常类似的表述。这里做一个补充说明：

定义$\mathcal{J}(\pi) = \mathbb{E}_{s_0, a_0, ...}[\sum_{t=0}^{\infty}\gamma^tr(s_t)]$。

则策略$\bar{\pi}$相比于旧策略$\pi$的期望收益为：

$\begin{aligned} \eta(\bar{\pi}) &=\mathcal{J}(\bar{\pi}) - \mathcal{J}(\pi) \\ &= \sum_s\rho_{\bar{\pi}}(s)\sum_a\bar{\pi}(a|s)A_{\pi}(s, a)\\ &= \mathbb{E}_{s, a\sim \bar{\pi}}[A_{\pi}(s, a)] \end{aligned}$

考虑到$\bar{\pi}$和$\pi$不能离得太远，因此加上限制条件： $\begin{aligned} D_{KL}(\bar{\pi}||\pi) &= \sum_s\sum_a\bar{\pi}(a|s)\log\frac{\bar{\pi}(a|s)}{\pi(a|s)}\leq \epsilon \end{aligned}$

这样对比下来，TDPO的目标也就清楚多了。

用拉格朗日的方式转化以下TDPO的目标式子，得到： $\begin{aligned} \max_{\theta} \mathbb{E}_{[x, y^{<t}],z\sim\pi_{\theta}([x, y^{<t}])}[A_{\pi_{ref}}([x, y^{<t}], z) - \beta D_{KL}(\pi_{\theta}([x, y^{<t}])||\pi_{ref}[x, y^{<t}])] \end{aligned}$

这个期望为双重期望的形式，我们取出一层进行分析，我们将$[x, y^{<t}]$简记为s, z即为a，固定s，我们需要最大化： $\begin{aligned} \max_{\theta} \mathbb{E}_{a\sim\pi_{\theta}(s)}[A_{\pi_{ref}}(s, a)] - \beta D_{KL}(\pi_{\theta}(s)||\pi_{ref}(s)) \end{aligned}$

我们先暂时抛开这个式子的求解，进入一个一般化的数学问题。

玻尔兹曼分布

还记得在soft q-learning中的一般化的数学问题吗？

待求解问题： $\max_{\mu} \mathbb{E}_{x\sim \mu(x)}[f(x)] + H(\mu), s.t.\sum_x\mu(x)=1$

该式的最优解服从： $\mu(x) = \frac{e^{ f(x)}}{\sum_xe^{ f(x)}}$

回过头来看一下 $\begin{aligned} &\max_{\theta}\mathbb{E}_{a\sim\pi_{\theta}(s)}[A_{\pi_{ref}}(s, a)] - \beta D_{KL}(\pi_{\theta}(s)||\pi_{ref}(s))\\ &=\max_{\theta} \mathbb{E}_{a\sim\pi_{\theta}(s)}[A_{\pi_{ref}}(s, a)] - \beta \sum_a\pi_{\theta}(a|s)\log\frac{\pi_{\theta}(a|s)}{\pi_{ref}(a|s)}\\ &=\max_{\theta} \mathbb{E}_{a\sim\pi_{\theta}(s)}[A_{\pi_{ref}}(s, a) + \beta {\log\pi_{ref}(a|s)}] + \beta H(\pi_{\theta}(s)) \end{aligned}$

即最优解： $\begin{aligned} \pi^*_{\theta}(a|s) &= \frac{e^{ A_{\pi_{ref}}(s, a)+ \beta {\log\pi_{ref}(a|s)}}} {\sum_a e^{ A_{\pi_{ref}}(s, a)+ \beta {\log\pi_{ref}(a|s)}}}\\ &= \frac{\pi_{ref}(a|s)e^{\frac{1}{\beta}A_{\pi_{ref}}(s, a)}}{\sum_a \pi_{ref}(a|s)e^{\frac{1}{\beta}A_{\pi_{ref}}(s, a)}}\\ &= \frac{\pi_{ref}(a|s)e^{\frac{1}{\beta}Q_{\pi_{ref}}(s, a)}}{\sum_a \pi_{ref}(a|s)e^{\frac{1}{\beta}Q_{\pi_{ref}}(s, a)}}\\ &= \frac{\pi_{ref}(a|s)e^{\frac{1}{\beta}Q_{\pi_{ref}}(s, a)}}{Z(s)} \end{aligned}$

其中最后一步的是因为$A=Q-V$而V只与s有关，在s固定的情况下，分子分母同时除以$e^{\frac{1}{\beta}V(s)}$，因此最优解其实是Q在$\pi_{ref}(s)$下的玻尔兹曼分布。 当$\pi_{ref}(s)$为均匀分布时，此时最优解的闭式解与Soft Q-learning的Max Entropy Q-learning的解完全一样，$\pi^*\propto \exp(Q)$。

类似与DPO，我们将Q进行反表示： $\begin{aligned} Q_{\pi_{ref}}(s, a)=\beta\log\frac{\pi^*(a|s)}{\pi_{ref}(a|s)} + \beta \log Z(s) \end{aligned}$

用advantage代替r -> BT-model目标等价性

本节推导目标： $\sum_{t=1}^{T_1}A_{\pi}(s_w^t, y_w^t) - \sum_{t=1}^{T_2}A_{\pi}(s_l^t, y_l^t)=\sum_{t=1}^{T_1}r(s_t, y_w^t) - \sum_{t=1}^{T_2}r(s_t, y_l^t)$

截止到目前为止，TDPO的推导其实跟DPO的推导差不多，只不过TDPO因为降解到token-level，所以其最优化目标的期望为两层期望(s, a都需要求期望消除)，但是DPO的期望只包含一层期望。但是其最优策略的推导本质上都是一个加权的玻尔兹曼分布。

将最优化的目标进行替换之后，TDPO的BT-model优化目标也随之变化：

$P_{\mathrm{BT}}(y_{1}> y_{2}|x)=\sigma\left(\sum_{t=1}^{T_{1}}\gamma^{t-1}A_{\pi}([x,y_{1}^{<t}],y_{1}^{t})-\sum_{t=1}^{T_{2}}\gamma^{t-1}A_{\pi}([x,y_{2}^{<t}],y_{2}^{t})\right)$

证明：

$\begin{aligned} &\ \ \ \ \sum_{t=1}^{T_1}A_{\pi}(s_w^t, y_w^t) - \sum_{t=1}^{T_2}A_{\pi}(s_l^t, y_l^t)\\ &=\sum_{t=1}^{T_1}\Big(r(s_w^t, y_w^t) + V_{\pi}(s_w^{t+1}) - V_{\pi}(s_w^t)\Big) - \sum_{t=1}^{T_2}\Big(r(s_l^t, y_l^t) + V_{\pi}(s_l^{t+1}) - V_{\pi}(s_l^t)\Big)\\ &=\sum_{t=1}^{T_1}r(s_w^t, y_w^t) - \sum_{t=1}^{T_2}r(s_l^t, y_l^t) + V_{\pi}(s_w^{T_1+1}) - V_{\pi}(s_l^{T_2+1}) - V_{\pi}(s_w^{1}) + V_{\pi}(s_l^{1})\\ \end{aligned}$

• EOS的影响，$V(s_w^{T_1+1}) =V(s_l^{T_2+1})$
• 一开始y都是空的，即$s_w^{1} = s_l^{1} = [x, y^{<1}] = [x]$，$V(s_w^{1}) = V(s_l^{1})$

因此： $\sum_{t=1}^{T_1}A_{\pi}(s_w^t, y_w^t) - \sum_{t=1}^{T_2}A_{\pi}(s_l^t, y_l^t)=\sum_{t=1}^{T_1}r(s_t, y_w^t) - \sum_{t=1}^{T_2}r(s_t, y_l^t)$

于是BT-model的优化目标的改写是合理的。

最终损失推导

本节推导目标： $\sum_{t=1}^T A_{\pi}(s_t, y_t) = \beta\sum_{t=1}^T\log\frac{\pi^*(y_t|s_t)}{\pi_{ref}(y_t|s_t)}+\beta\sum_{t=1}^T\pi_{ref}({y_t|s_t})\log\frac{\pi_{ref}(y_t|s_t)}{\pi^*({y_t|s_t})}$

证明：

$\begin{aligned} A_{\pi_{ref}}(s_t, y_t) &= Q_{\pi_{ref}}(s_t, y_t) - V_{\pi_{ref}}(s_t)\\ &= \beta\log\frac{\pi^*(y_t|s_t)}{\pi_{ref}(y_t|s_t)} + \beta\log Z(s_t) - \mathbb{E}_{y'\sim\pi_{ref}(s_t)}[\beta\log\frac{\pi^*(y'|s_t)}{\pi_{ref}(y'|s_t)} + \beta\log Z(s_t)]\\ &=\beta\log\frac{\pi^*(y_t|s_t)}{\pi_{ref}(y_t|s_t)}+ \beta D_{KL}(\pi_{ref}(s_t)||\pi^*(s_t)) \end{aligned}$

因此： $\sum_{t=1}^T A_{\pi}(s_t, y_t) = \beta\sum_{t=1}^T\log\frac{\pi^*(y_t|s_t)}{\pi_{ref}(y_t|s_t)}+\beta\sum_{t=1}^TD_{KL}(\pi_{ref}(s_t)||\pi^*(s_t))$

因此