GAIL: Generative Adversarial Imitation Learning

GAIL属于对抗模仿学习领域很重要的文章。本文的组织结构为：

GAIL的算法的流程和代码：What And How
GAIL的算法的原理: Why

本文的参考文献如下：

模仿学习简明教程

老规矩，我们还是先给出阅读本篇论文之前你应该阅读的文章或者了解的背景：

GAN论文 - GAIL的灵感来源
模仿学习的设定

GAIL这篇论文的逻辑链还是很有意思的，先根据GAN有算法设计灵感，实验效果又不错，再结合此前的对抗模仿学习(AIL, Adversarial Imitation Learning)的理论，最后得到了一个自洽的理论体系，建立起GAIL与AIL之间的connection，不可谓不精妙！

所以本文的结构也是这样组织的，先从实现出发，然后再从理论上去解释这个算法的合理性。 本文仅仅只是作为一个思维链的梳理，并不能代替读者去阅读原文，原文中定义的很多东西，比如occupancy measure等等，都是需要读者去仔细理解的。

GAN的铺垫

使用minist数据集，生成手写数字的代码示例：

GAN代码示例

import argparse
import os
import numpy as np
import math

import torchvision.transforms as transforms
from torchvision.utils import save_image

from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable

import torch.nn as nn
import torch.nn.functional as F
import torch

os.makedirs("images", exist_ok=True)

parser = argparse.ArgumentParser()
parser.add_argument("--n_epochs", type=int, default=200, help="number of epochs of training")
parser.add_argument("--batch_size", type=int, default=64, help="size of the batches")
parser.add_argument("--lr", type=float, default=0.0002, help="adam: learning rate")
parser.add_argument("--b1", type=float, default=0.5, help="adam: decay of first order momentum of gradient")
parser.add_argument("--b2", type=float, default=0.999, help="adam: decay of first order momentum of gradient")
parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation")
parser.add_argument("--latent_dim", type=int, default=100, help="dimensionality of the latent space")
parser.add_argument("--img_size", type=int, default=28, help="size of each image dimension")
parser.add_argument("--channels", type=int, default=1, help="number of image channels")
parser.add_argument("--sample_interval", type=int, default=400, help="interval betwen image samples")
opt = parser.parse_args()
print(opt)

img_shape = (opt.channels, opt.img_size, opt.img_size)

cuda = True if torch.cuda.is_available() else False


class Generator(nn.Module):
    def __init__(self):
        super(Generator, self).__init__()

        def block(in_feat, out_feat, normalize=True):
            layers = [nn.Linear(in_feat, out_feat)]
            if normalize:
                layers.append(nn.BatchNorm1d(out_feat, 0.8))
            layers.append(nn.LeakyReLU(0.2, inplace=True))
            return layers

        self.model = nn.Sequential(
            *block(opt.latent_dim, 128, normalize=False),
            *block(128, 256),
            *block(256, 512),
            *block(512, 1024),
            nn.Linear(1024, int(np.prod(img_shape))),
            nn.Tanh()
        )

    def forward(self, z):
        img = self.model(z)
        img = img.view(img.size(0), *img_shape)
        return img


class Discriminator(nn.Module):
    def __init__(self):
        super(Discriminator, self).__init__()

        self.model = nn.Sequential(
            nn.Linear(int(np.prod(img_shape)), 512),
            nn.LeakyReLU(0.2, inplace=True),
            nn.Linear(512, 256),
            nn.LeakyReLU(0.2, inplace=True),
            nn.Linear(256, 1),
            nn.Sigmoid(),
        )

    def forward(self, img):
        img_flat = img.view(img.size(0), -1)
        validity = self.model(img_flat)

        return validity


# Loss function
adversarial_loss = torch.nn.BCELoss()

# Initialize generator and discriminator
generator = Generator()
discriminator = Discriminator()

if cuda:
    generator.cuda()
    discriminator.cuda()
    adversarial_loss.cuda()

# Configure data loader
os.makedirs("../../data/mnist", exist_ok=True)
dataloader = torch.utils.data.DataLoader(
    datasets.MNIST(
        "../../data/mnist",
        train=True,
        download=True,
        transform=transforms.Compose(
            [transforms.Resize(opt.img_size), transforms.ToTensor(), transforms.Normalize([0.5], [0.5])]
        ),
    ),
    batch_size=opt.batch_size,
    shuffle=True,
)

# Optimizers
optimizer_G = torch.optim.Adam(generator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
optimizer_D = torch.optim.Adam(discriminator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))

Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor

# ----------
#  Training
# ----------

for epoch in range(opt.n_epochs):
    for i, (imgs, _) in enumerate(dataloader):

        # Adversarial ground truths
        valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
        fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)

        # Configure input
        real_imgs = Variable(imgs.type(Tensor))

        # -----------------
        #  Train Generator
        # -----------------

        optimizer_G.zero_grad()

        # Sample noise as generator input
        z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))

        # Generate a batch of images
        gen_imgs = generator(z)

        # Loss measures generator's ability to fool the discriminator
        g_loss = adversarial_loss(discriminator(gen_imgs), valid)

        g_loss.backward()
        optimizer_G.step()

        # ---------------------
        #  Train Discriminator
        # ---------------------

        optimizer_D.zero_grad()

        # Measure discriminator's ability to classify real from generated samples
        real_loss = adversarial_loss(discriminator(real_imgs), valid)
        fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake)
        d_loss = (real_loss + fake_loss) / 2

        d_loss.backward()
        optimizer_D.step()

        print(
            "[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
            % (epoch, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item())
        )

        batches_done = epoch * len(dataloader) + i
        if batches_done % opt.sample_interval == 0:
            save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)

GAIL的算法的流程和代码

伪代码：

TRPO相对比较难实现，因此我们在PPO的基础上添加了一个Discriminator，用来判别专家策略和生成策略的区别。除了rewards的信号来源来自于Discriminator的输出外，其它与PPO基本一致。

代码实现详见这里

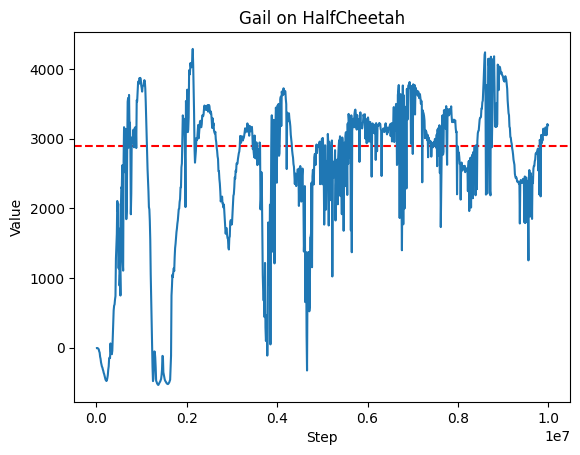
代码实现得比较简单，只在HalfCheetah环境上进行了测试，做了一个简单实验验证了GAIL的效果。

关键代码：

GAN代码示例

class GAILAgent:
    # ...

    def update_discriminator(self, exp_obs, exp_act, obs, act):
        # train discriminator
        # get expert and agent logits
        expert_logits = self.discriminator.get_logits(exp_obs, exp_act)
        agent_logits = self.discriminator.get_logits(obs, act)

        # compute discriminator loss
        expert_loss = F.binary_cross_entropy(
            expert_logits, torch.ones_like(expert_logits)
        )
        agent_loss = F.binary_cross_entropy(
            agent_logits, torch.zeros_like(agent_logits)
        )
        discriminator_loss = expert_loss + agent_loss

        # step discriminator
        self.discriminator_optimizer.zero_grad()
        discriminator_loss.backward()
        self.discriminator_optimizer.step()

        return {
            "loss/discriminator": discriminator_loss.item(),
            "loss/d_expert": expert_loss.item(),
            "loss/d_agent": agent_loss.item(),
        }

    def update(self, data_batch):
        (
            obs_batch,
            action_batch,
            reward_batch,
            next_obs_batch,
            done_batch,
            truncated_batch,
        ) = itemgetter("obs", "action", "reward", "next_obs", "done", "truncated")(
            data_batch
        ) # The actual reward is not used in the training process

        # get reward from discriminator
        discriminator_reward_batch = torch.log(
            self.discriminator(obs_batch, action_batch) + 1e-8
        ).detach()
        assert discriminator_reward_batch.shape == reward_batch.shape
        advantage_batch, return_batch = self.estimate_advantage(
            obs_batch,
            action_batch,
            discriminator_reward_batch,
            next_obs_batch,
            done_batch,
            truncated_batch,
        )
        with torch.no_grad():
            log_prob_batch = itemgetter("log_prob")(
                self.policy_network.evaluate_actions(obs_batch, action_batch)
            )

        # update policy
        update_policy_counts = 0
        for update_policy_step in range(self.train_policy_iters):
            # compute and step policy loss
            new_log_prob, dist_entropy = itemgetter("log_prob", "entropy")(
                self.policy_network.evaluate_actions(obs_batch, action_batch)
            )

            ratio_batch = torch.exp(new_log_prob - log_prob_batch)
            approx_kl = (log_prob_batch - new_log_prob).mean().item()
            if approx_kl > 1.5 * self.target_kl:
                break
            if self.policy_loss_type == "clipped_surrogate":
                surrogate1 = advantage_batch * ratio_batch
                # print(self.clip_range, advantages.shape, ratio_batch.shape)
                surrogate2 = advantage_batch * torch.clamp(
                    ratio_batch, 1.0 - self.clip_range, 1.0 + self.clip_range
                )
                policy_loss = -(torch.min(surrogate1, surrogate2)).mean()
            elif self.policy_loss_type == "naive":
                raise NotImplementedError
            elif self.policy_loss_type == "adaptive_kl":
                raise NotImplementedError

            # entropy loss
            entropy_loss = -dist_entropy.mean() * self.entropy_coeff
            entropy_loss_value = entropy_loss.item()
            entropy_val = dist_entropy.mean().item()
            policy_loss_value = policy_loss.item()
            tot_policy_loss = policy_loss + entropy_loss

            self.policy_optimizer.zero_grad()
            tot_policy_loss.backward()
            self.policy_optimizer.step()
            update_policy_counts += 1

        for update_v_step in range(self.train_v_iters):
            # compute value loss
            curr_state_v = self.v_network(obs_batch)
            v_loss = F.mse_loss(curr_state_v, return_batch)
            self.v_optimizer.zero_grad()
            v_loss.backward()
            self.v_optimizer.step()
            v_loss_value = v_loss.detach().cpu().numpy()

        if update_policy_counts > 0:
            return {
                "loss/v": v_loss_value,
                "loss/policy": policy_loss_value,
                "loss/entropy": entropy_loss_value,
                "misc/entropy": entropy_val,
                "misc/kl_div": approx_kl,
                "misc/policy_updates": update_policy_counts,
            }
        else:
            return {
                "loss/v": v_loss_value,
                "misc/kl_div": approx_kl,
                "misc/policy_updates": update_policy_counts,
            }

GAIL的算法的原理

一个定理

抛开一切GAIL的内容，我们来看一个定理：

第一次看这个定理确实感觉不太好理解，因此，我们在这里给出证明：

原问题即证明：

$\forall y, \max_{\|z \|_* \leq 1} z^\top y = \|y\|$

case 1

当 $\|y\|$ 为 $1$ 维时，对于 $z$ 的每一个分量 $z_i$ ，有 $|z_i| \leq 1$ ；当 $z_i y_i = |y_i|$ 时， $z^\top y = \|y\|$ ，显然此时最大。

case 2

当 $\|y\|$ 为无穷维时，对于 $z$ 的每一个分量 $z_i$ ，有 $\sum |z_i| \leq 1$ ；当 $y$ 绝对值最大的分量 $y_j$ 对应的 $z_j$ 满足 $z_j y_j = |y_j|$ 时， $z^\top y = \|y\|$ ，显然此时最大。

case 3

设 $\|y\|$ 为 $p$ 维，设 $\|z \|_*$ 为 $q$ 维，其中 $\frac{1}{p} + \frac{1}{q} = 1$ ；不妨设 $y, z$ 有 $n$ 维，且所有分量均为非负数。

问题转化为证明如下不等式成立且可以取到等号：

$\sum y_i z_i \leq \left(\sum y_i ^ p \right)^{\frac{1}{p}} \cdot \left(\sum z_i ^ q \right)^{\frac{1}{q}}$

这实际上是 Holder 不等式，证明如下：首先有引理：根据对数函数 $\ln (x)$ 的凹凸性有：

$\ln \left(\frac{1}{p} a + \frac{1}{q} b\right) \geq \frac{1}{p} \ln a + \frac{1}{q} \ln b$

故：

$a ^ \frac{1}{p} b^ \frac{1}{q} \leq \frac{1}{p} a + \frac{1}{q} p$ 代入 $a = \frac{y_i ^ p}{\sum_{i=1} ^ n y_i ^p}, b = \frac{z_i ^ q}{\sum_{i=1} ^ n z_i ^q}$ 有：

$\frac{y_i z_i}{\left(\sum_{i=1} ^ n y_i ^p\right) ^ \frac{1}{p} {\left(\sum_{i=1} ^ n z_i ^q\right) ^ \frac{1}{q} }} \leq \frac{1}{p } \frac{y_i ^ p}{\sum_{i=1} ^ n y_i ^p} + \frac{1}{q} \frac{z_i ^ q}{\sum_{i=1} ^ n z_i ^q}$

全部加起来，

$\frac{\sum_{i=1} ^n y_i z_i}{\left(\sum_{i=1} ^ n y_i ^p\right) ^ \frac{1}{p} {\left(\sum_{i=1} ^ n z_i ^q\right) ^ \frac{1}{q} }} \leq \frac{1}{p} + \frac{1}{q} = 1$

即：

$\sum y_i z_i \leq \left(\sum y_i ^ p \right)^{\frac{1}{p}} \cdot \left(\sum z_i ^ q \right)^{\frac{1}{q}}$

极大极小优化建模

给定专家策略E，我们的优化目标为： $\text{minimize}_{\pi} d_{\psi}(\rho_{\pi}, \rho_{E}) - H(\pi)$

其中 $d_{\psi}(\rho_{\pi}, \rho_{E})$ 是一个距离函数，用来衡量 $\rho_{\pi}$ 和 $\rho_{E}$ 之间的差异， $H(\pi)$ 是策略的熵。这个优化问题的目标是找到一个策略 $\pi$ ，使得 $\rho_{\pi}$ 和 $\rho_{E}$ 之间的差异最小，同时策略的熵最大。

我们在后面的分析中，暂时不考虑 $H(\pi)$ 这一项。

给出几个常用的距离函数：

TV-distance: $d_{TV}(\rho_{\pi}, \rho_{E}) = \frac{1}{2} \sum_{(s, a)\in S\times \mathcal{A}}|p_{\pi}(s, a) - p_{E}(s, a)|$ ，可以看到，其实TV距离跟L1范数是等价的。
KL-divergence: $d_{KL}(\rho_{\pi}, \rho_{E}) = \sum_{(s, a)\in S\times \mathcal{A}}p_{\pi}(s, a) \log \frac{p_{\pi}(s, a)}{p_{E}(s, a)}$
Jensen-Shannon divergence: $d_{JS}(\rho_{\pi}, \rho_{E}) = \frac{1}{2} d_{KL}(\rho_{\pi}, \rho_{\mu}) + \frac{1}{2} d_{KL}(\rho_{E}, \rho_{\mu})$

其中 $\rho_{\mu} = \frac{1}{2}(\rho_{\pi} + \rho_{E})$

针对TV-distance，我们可以得到如下的优化问题： $\text{minimize}_{\pi} \frac{1}{2} \sum_{(s, a)\in S\times \mathcal{A}}|p_{\pi}(s, a) - p_{E}(s, a)|$ 根据上一小节的定理，我们可以将上述问题转化为一个极小极大问题： $\text{minimize}_{\pi} \text{max}_{w} \sum_{(s, a)\in S\times \mathcal{A}}w(s, a) (p_{\pi}(s, a) - p_{E}(s, a))$ 其中 $w\in \mathbb{R}^{|S\times \mathcal{A}|}, ||w||_{\infty} \leq 1$ ，我这里偷懒省略了time-step的下标。具体可以参考模仿学习简明教程。

在GAIL中，我们使用的是Jensen-Shannon divergence，因此我们的优化问题为： $\text{minimize}_{\pi} D_{JS}(\rho_{\pi}, \rho_{E})$ 根据Jensen-Shannon divergence的对偶形式，我们可以得到以下的极小极大问题，这个目标跟GAN看起来还是类似的： $\text{minimize}_{\pi} \max_{S\times \mathcal{A}} \mathbb{E}_{\rho_{\pi}}[\log D_{\phi}(s, a)] + \mathbb{E}_{\rho_{E}}[\log(1 - D_{\phi}(s, a))]$

你看到这里可能会觉得很奇怪，Jensen-Shannon divergence的对偶形式并不是那么容易就得到，GAIL作者难道是先从Jensen-Shannon divergence出发，然后推导出了这个极小极大问题吗？最后才得出一个类似于GAN的形式？

实际上并不是这样的，GAIL的作者是先从一个类似于GAN的形式出发，然后推导出了Jensen-Shannon divergence。所以相当于是先从GAN获得了算法实现的motivation，然后再从理论上证明了这个算法的合理性。

GAIL