IQL: Offline Reinforcement Learning with Implicit Q-Learning

IQL的作者之一是：Ilya Kostrikov，也是我们熟知的DRQ的作者。

以及Sergey Levine，SAC和TRPO都与其相关：

SARSA

SARSA是一个经典的RL算法，考虑数据集给出的五元组$(s_t, a_t, r_t, s_{t+1}, a_{t+1})$， 它的更新公式如下： $Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left( r_t + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t) \right)$

损失函数为： $L(\theta) = \mathbb{E}_{(s, a, r, s', a') \sim D} \left[ \left( Q(s, a) - (r + \gamma Q(s', a')) \right)^2 \right]$

相比于比较常见的更新时使用四元组$(s_t, a_t, r_t, s_{t+1})$，SARSA使用了五元组，这样的好处是可以直接避免了action ood的情况。

TODO: 添加缺点分析

函数拟合？

我们对上面的目标稍作修改： $L(\theta) = \mathbb{E}_{(s, a, r, s')} \left[ r + \gamma \max_{a'\in \mathcal{A},\pi^{\beta}(a'|s')>0} Q(s', a'; \theta) - Q(s, a; \theta) \right]^2$

这里的$\pi^{\beta}(a'|s')>0$表示在数据集中$a'$的概率大于0，也就是说，我们只考虑数据集中的action。$\pi^{\beta}$跟之前几篇博文的含义一致，表示行为策略，实际表示的是数据集中的行为分布。

你可能会问$\max_{a'\in A, s.t.\pi_{\beta}(a'|s')>0} Q(s', a')$这个式子要怎么估计，毕竟$\pi^{\beta}$未知，我们每次采样的也仅仅是四元组$(s, a, r, s')$，完全不知道$a'$对应的分布。

这个问题也就是IQL的核心问题，一言以蔽之：

函数拟合！！！我们用一个函数$f(s')$拟合$\max_{a'\in A, s.t.\pi_{\beta}(a'|s')>0} Q(s', a')$，然后用这个函数来更新Q函数。

为了统一表示，我们后文使用$V(s')$来表示$f(s')$。即： $V(s') = \max_{a'\in A, s.t.\pi_{\beta}(a'|s')>0} Q(s', a')$

说起来挺简单，但关键就在于如何拟合这个函数。先别急，我们来看一个更加一般化的建模问题。

一般化的建模问题

假设我们现在有一个二元函数 F(x, y)，不知道它的具体表达式，现在允许你每次从集合$D$中选取并输入一个二元组(x1, x2)，从而获取F(x1, x2)的值。

我们现在想拟合一个函数G(x)，使得$G(x)=\max_{y} F(x, y)$。

使用神经网络拟合G(x1)，假设某一次更新时，假设我们现在拿到一个pair(x1, x2)

• $F(x_1, x_2)-G(x_1) > 0$，那显然G(x1)肯定还需要增大，否则不能满足最大化的要求，此时loss > 0，一个显然的方式是将$(F(x_1, x_2)-G(x_1))^2$作为Loss，毕竟值回归用MSE作为损失，简直是太常见了；
• $F(x_1, x_2)-G(x_1)\leq 0$，那么我们希望此时Loss最好等于 = 0，或者是一个比较小的数值，这是因为此前的更新已经使得G(x1)足够大，不需要再继续增大了。

ok，讲到这里，我们开始引入损失函数：

$L_{\tau}(u) = |\tau - I(u<0)| u^2$

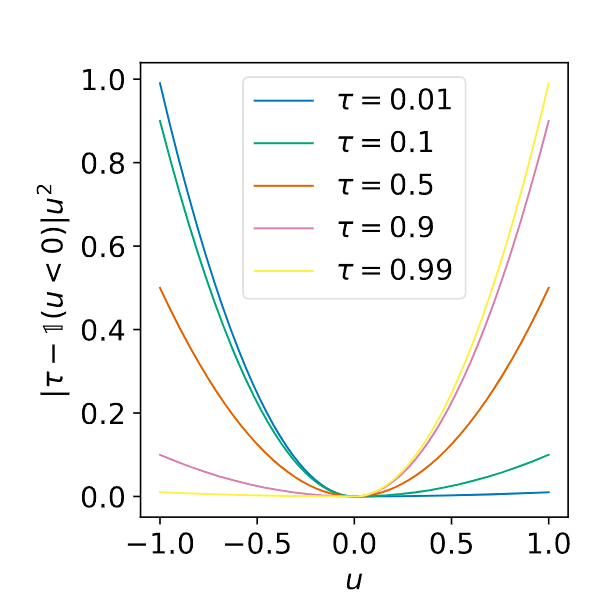
这里的I是指示函数，如果u<0，那么I(u<0)=1，否则I(u<0)=0。当$\tau=0.5$时，这个损失函数就是一个标准的MSE损失函数。当$\tau\ne0.5$时，这个函数为非对称的MSE。 这里的$\tau$是一个设定好的超参数，在(0,1)之间，这里的u其实就是我们前面的$F(x_1, x_2)-G(x_1)$。

不同的超参数$\tau$的选取，对损失函数的影响如下：

至此，我们回过头来看看V(s')的拟合问题，你是不是有了一些灵感？

V(s')的拟合

我们的目标是拟合V(s')，使得$V(s') = \max_{a'\in A, s.t.\pi_{\beta}(a'|s')>0} Q(s', a')$。

记作V的参数为$\phi$，则损失： $L_{V}(\phi) = \mathbb{E}_{(s, a)\sim \mathcal{D}} L_{\tau} \left( Q(s, a) - V(s) \right)$

这里的$\mathcal{D}$是数据集，$\tau$是一个超参数，用来控制对于正负误差的惩罚程度。

所以IQL整体的更新方式，写成batch-update的形式：

    def continuous_action_space_update(self, data_batch):
        (
            obs_batch,
            action_batch,
            reward_batch,
            next_obs_batch,
            done_batch,
            truncated_batch,
        ) = itemgetter("obs", "action", "reward", "next_obs", "done", "truncated")(
            data_batch
        )

        reward_batch = reward_batch * self.reward_scale

        with torch.no_grad():
            q = self.target_q_network([obs_batch, action_batch])
            target_q = self.v_network(next_obs_batch)
            target_q = reward_batch + self.gamma * (1.0 - done_batch) * target_q

        # 1. compute q loss and backward
        q1, q2 = self.q_network.both([obs_batch, action_batch])
        q_loss = (F.mse_loss(q1, target_q) + F.mse_loss(q2, target_q)) * 0.50
        self.q_optimizer.zero_grad(set_to_none=True)
        q_loss.backward()
        self.q_optimizer.step()

        # 2. calculate v loss
        v_value = self.v_network(obs_batch)
        adv = q - v_value
        v_loss = asymmetric_l2_loss(adv, self.tau)

        self.v_optimizer.zero_grad(set_to_none=True)
        v_loss.backward()
        # clip_grad_norm_(self.v_network.parameters(), max_norm=1.0)
        self.v_optimizer.step()

        # 3. calculate policy loss
        exp_adv = torch.exp(self.beta * adv.detach()).clamp(max=EXP_ADV_MAX)
        policy_logp = self.policy_network.evaluate_actions(obs_batch, action_batch)[
            "log_prob"
        ]
        policy_loss = -torch.mean(exp_adv * policy_logp)

        self.policy_optimizer.zero_grad(set_to_none=True)
        policy_loss.backward()
        self.policy_optimizer.step()

        # 4. soft update target network
        self.soft_update()

        return {
            "loss/q_loss": q_loss.item(),
            "loss/v_loss": v_loss.item(),
            "loss/policy_loss": policy_loss.item(),
            "value/q_value": q.mean().item(),
            "value/v_value": v_value.mean().item(),
        }

除了V的拟合采用了非对称的MSE，Q值的学习在得到V之后就很容易了，而训练得到V和Q之后，参考AWR或者AWAC的思路，我们可以得到一个新的行为策略，这个策略的形式是： $\pi(a|s) = \frac{\exp(\beta(Q(s, a) - V(s)))}{\sum_{a'}\exp(\beta(Q(s, a') - V(s)))}$ ，策略学习的细节部分可以参考AWAC的文章。

实验结果

TODO: 补充自己的实验效果

总结

IQL的核心思想是通过拟合一个函数V(s')来近似$\max_{a'\in A, s.t.\pi_{\beta}(a'|s')>0} Q(s', a')$，从而避免了action ood的问题。拟合的方式采用了非对称的MSE，通过调整超参数$\tau$来控制对于正负误差的惩罚程度。

终极奥义：一个最大化的函数拟合，非对称的MSE！