TD3+BC: A Minimalist Approach to Offline Reinforcement Learning

本文是Google Brain团队和McGill大学合作，由 TD3、BCQ的作者 Fujimoto 提出并发表在NeurIPS2021顶会上的文章，本文方法最大的优点是：方法简单、无任何复杂数学公式、可实现性强(开源)、对比实验非常充分（满分推荐），正如标题一样(A minimalist approach)。

算法内容

对于经典的DDPG、TD3等算法来讲， 策略梯度的计算根据David sliver提出的如下定义，即求解状态-动作值函数的期望值：

$\pi=\arg \max _{\pi} \mathbb{E}_{s \sim \rho_{\pi}, a \sim \pi}\left[Q_{\pi}(s, a)\right]$

本文中，作者为了尽可能的让两个动作接近添加了一个正则项$\pi(s) - a$，即： $\pi=\arg \max _{\pi} \mathbb{E}_{s \sim \rho_{\pi}, a \sim \pi}\left[Q_{\pi}(s, a) - \left\|\pi(s) - a\right\|^{2}\right]$

另外一个技术点就是从代码执行层面的优化，即Normalize State，具体的Normalize过程如公式所示：

$s_{i}=\frac{s_{i}-\mu_{i}}{\sigma_{i}+\epsilon}$

最后一个技术点就是关于 λ\lambda\lambda 的求解，作者给出了计算公式，并在后文中说取值为 λ=2.5\lambda=2.5\lambda=2.5 的时候效果最好， 实验部分有作者做的ablation实验证明 $\lambda=\frac{\alpha}{\frac{1}{N} \sum_{\left(s_{i}, a_{i}\right)}\left|Q\left(s_{i}, a_{i}\right)\right|}$

代码也是相当之简洁：

    def train(self, replay_buffer, batch_size=256):
        self.total_it += 1

        # Sample replay buffer 
        state, action, next_state, reward, not_done = replay_buffer.sample(batch_size)

        with torch.no_grad():
            # Select action according to policy and add clipped noise
            noise = (
                torch.randn_like(action) * self.policy_noise
            ).clamp(-self.noise_clip, self.noise_clip)

            next_action = (
                self.actor_target(next_state) + noise
            ).clamp(-self.max_action, self.max_action)

            # Compute the target Q value
            target_Q1, target_Q2 = self.critic_target(next_state, next_action)
            target_Q = torch.min(target_Q1, target_Q2)
            target_Q = reward + not_done * self.discount * target_Q

        # Get current Q estimates
        current_Q1, current_Q2 = self.critic(state, action)

        # Compute critic loss
        critic_loss = F.mse_loss(current_Q1, target_Q) + F.mse_loss(current_Q2, target_Q)

        # Optimize the critic
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()

        # Delayed policy updates
        if self.total_it % self.policy_freq == 0:

            # Compute actor loss
            pi = self.actor(state)
            Q = self.critic.Q1(state, pi)
            lmbda = self.alpha/Q.abs().mean().detach()

            actor_loss = -lmbda * Q.mean() + F.mse_loss(pi, action) 

            # Optimize the actor 
            self.actor_optimizer.zero_grad()
            actor_loss.backward()
            self.actor_optimizer.step()

            # Update the frozen target models
            for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()):
                target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

            for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
                target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

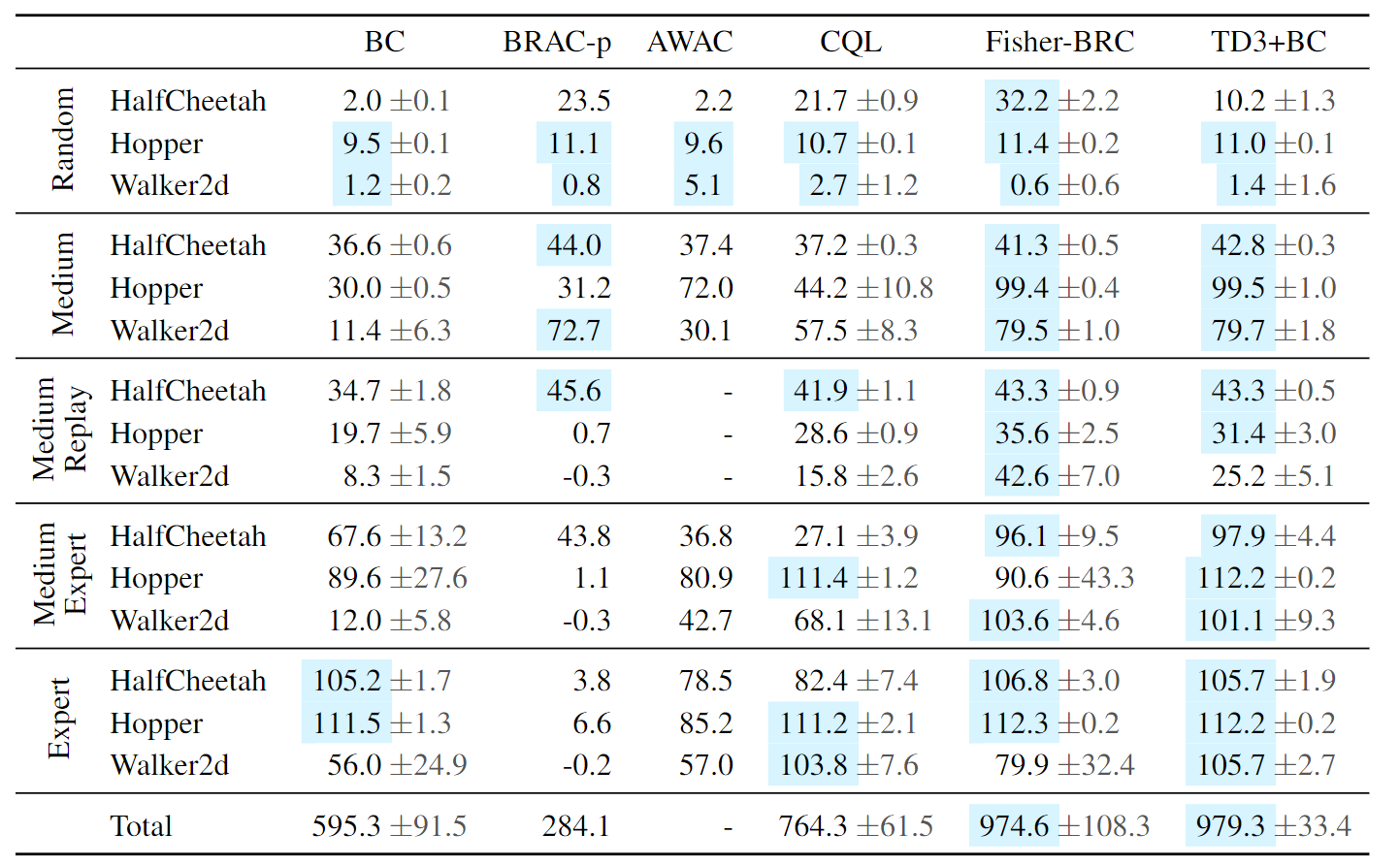
实验结果